剪切长方体盒子后的角与边数量探秘——烧脑大作战137关深度解析
在烧脑大作战的第137关中,我们面临一个看似简单实则充满挑战的问题:剪切一个具有8个角和8条边的长方体盒子后,它还会剩下多少个角和多少条边?这个问题不仅考验了我们对几何图形的理解,还挑战了我们的空间想象能力和逻辑推理能力,我们将通过详细的分析和推理,来解答这个问题,并探讨其背后的几何原理。
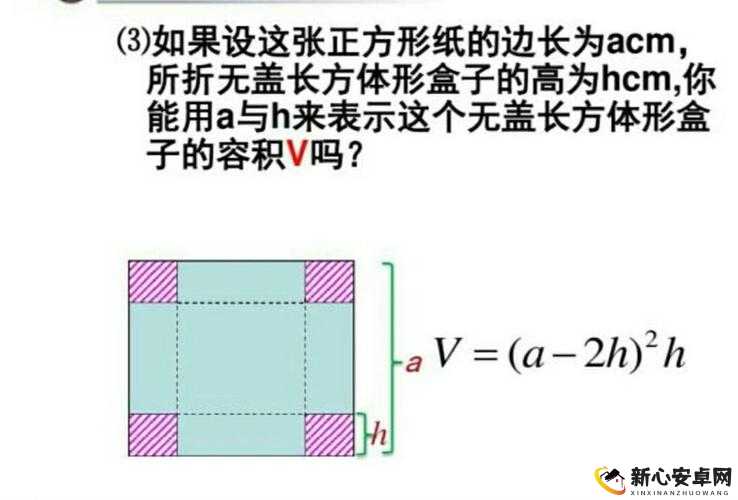
一、长方体盒子的基本特征
我们需要明确长方体盒子的基本特征,一个标准的长方体盒子有6个面、8个角和12条边,每个角由三条边相交而成,而每条边则连接两个相邻的面,在三维空间中,长方体的这些特征共同构成了一个封闭、规则的几何体。
二、剪切操作的几何影响
我们分析剪切操作对长方体盒子几何特征的影响,剪切操作通常意味着沿着某个平面或曲线切割物体,从而改变其形状和边界,对于长方体盒子来说,剪切操作可能涉及以下几种情况:
1、沿边剪切:如果剪切线沿着长方体的某条边进行,那么这条边将被分割成两段,同时产生一个新的角(或两个,取决于剪切线的具体形状),由于长方体盒子的封闭性,这种剪切通常会导致盒子被分割成两个或多个部分,除非剪切线恰好形成一个封闭的环(如沿着盒子的一个面进行剪切)。
2、沿面剪切:如果剪切线沿着长方体的某个面进行,那么这个面将被分割成两部分,同时产生一条新的边(或更多,取决于剪切线的复杂性),这种剪切通常不会改变角的数量,但会改变边的数量和形状。
3、复杂剪切:除了沿边和面进行简单的剪切外,还可以进行更复杂的剪切操作,如沿着非直线或曲面进行剪切,这些操作可能导致更复杂的几何变化,包括角的增加或减少、边的断裂和重新连接等。
三、具体剪切情况分析
我们回到原问题:剪切一个具有8个角和8条边的长方体盒子(注意这里的“8条边”实际上是指长方体在三维空间中连接不同面的边数,而不是指每个面的边数),由于题目没有明确指出剪切线的具体位置和形状,我们只能进行一般性的分析。
1、如果剪切线沿着长方体的某条边进行:
- 角的数量可能会增加(如果剪切线不封闭),也可能会保持不变(如果剪切线封闭且没有穿过其他角)。
- 边的数量会增加(因为每条被剪切的边都会变成两条)。
2、如果剪切线沿着长方体的某个面进行:
- 角的数量通常保持不变(除非剪切线穿过其他角)。
- 边的数量会增加(因为剪切线会分割出更多的边)。
3、复杂剪切情况:
- 在这种情况下,角和边的数量变化将取决于剪切线的具体形状和位置。
- 剪切操作可能会导致角的增加或减少(如果剪切线穿过角)、边的增加(因为剪切线会分割出更多的边)以及边的重新连接(如果剪切线形成复杂的形状)。
四、结论与推理
由于题目没有给出具体的剪切方式和位置,我们无法给出一个确定的答案,我们可以根据几何原理进行推理:
- 在任何剪切操作中,如果剪切线不穿过任何角,那么角的数量将保持不变(8个)。
- 如果剪切线穿过一个或多个角,那么每穿过一个角,就会增加或减少一个角(取决于剪切线的方向)。
- 边的数量通常会增加,因为剪切线会分割出更多的边,如果剪切线形成封闭的环(如沿着长方体的一个面进行剪切),并且没有穿过任何额外的边,那么边的总数可能不会改变(仍然是8条,但每条边都被重新定义了)。
一个合理的结论是:剪切一个具有8个角和8条边的长方体盒子后,角和边的数量将取决于剪切线的具体位置和形状,在没有具体信息的情况下,我们无法确定最终的角和边数。
五、相关问题及解答
问题:如果沿着长方体盒子的一个面进行直线剪切,使其恰好将这个面分成两个相等的部分,那么剪切后的盒子将有多少个角和多少条边?
解答:
1、角的数量:由于剪切线沿着长方体的一个面进行,并且没有穿过任何角,因此角的数量保持不变,剪切后的盒子仍然有8个角。
2、边的数量:剪切线将长方体盒子的一个面分成两个相等的部分,这意味着这条剪切线将成为一条新的边,被剪切的面上的原有边将被分割成两段,由于长方体盒子的封闭性,这条新的边实际上与长方体盒子的其他边相连,形成了新的边界,在三维空间中观察,边的总数并没有增加(仍然是连接不同面的8条边,但每条边的位置和长度可能发生了变化),如果我们考虑剪切后形成的两个独立部分(如果它们没有重新连接的话),那么每个部分都将有自己的边数(可能大于8条,因为剪切面内部的边也被计算在内了),根据题目的原始要求(即考虑整个剪切后的盒子),我们仍然认为边的总数是8条(在三维空间中的连接不同面的边数)。
如果沿着长方体盒子的一个面进行直线剪切,使其恰好将这个面分成两个相等的部分,那么剪切后的盒子在三维空间中仍然有8个角和8条连接不同面的边(但内部结构和边界可能发生了变化)。